常说的QQ图究竟是怎么来的，QQ图有何意义。今天我们来了解QQ图~

1.基础知识

• 分位数(Quantile)，亦称分位点，是指将一个随机变量的概率分布范围分为几个等份的数值点，常用的有中位数(即二分位数)、四分位数、百分位数等。在实际运用中，可以根据数据的情况，确定其他的分位数，如七分位数、八分位数等等。

• 四分位数(Quartile)，即统计学中，把所有数值由小到大排列并分成四等份，处于三个分割点位置的得分就是四分位数。

  • 第一四分位数 (Q1)，又称“较小四分位数”，等于该样本中所有数值由小到大排列后第25%的数字。
  • 第二四分位数 (Q2)，又称“中位数”，等于该样本中所有数值由小到大排列后第50%的数字。
  • 第三四分位数 (Q3)，又称“较大四分位数”，等于该样本中所有数值由小到大排列后第75%的数字。
  • 第三四分位数与第一四分位数的差距又称四分位距(InterQuartile Range,IQR)。

2.分位数计算简单举例

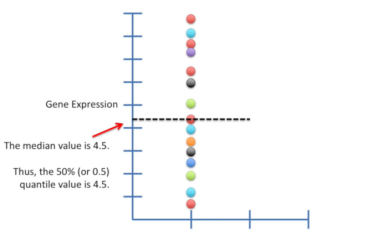
50%分位数：如测量15个基因的表达水平。在中位值将数据平均分成2份，50%基因的表达量高于该值，50%基因的表达量低于该值。故中位值为分位数，可将它标记为0.5或50%分位数。计算得出中位数值为4.5，故50%(0.5)分位数的值为4.5。

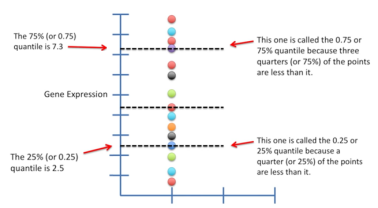
25%和75%分位数：在中位数值的基础上，继续添加两个值，将数据进行四等分。新添加的值也是分位数，因为其将数据平均分为4份。较小四分位数(最小的一个值)2.5为25%(0.25)分位数，因为25%的数据小于2.5；较大四分位数(最大的一个值)7.3位75%(0.75)分位数，因为75%的数据小于7.3。

综合以上，我们可以进行简单总结：将数据等分的数值为分位数，它们可将数据进行2等分、3等分、4等分......百分位数(percentile)将数据100等分。

❝

R中quantile()函数提供了9中计算分位数的方法，各方法得出的结论是否相似与样本含量有关。

具体而言，如果是小样本量的数据，9种方法得出的结果可能有较大的差别；如果是大样本量的数据，9种方法得出的结果可能非常相似。

❞

3. 分位数与QQ图

在实际运用中，分位数的运用非常灵活，且不同分位数之间可以具有相同的意义。

• 尽管在只有15个数据的样本中，我们仍然能将数据平均分成100份，中位数值为50%分位数，较小四分位数为25%分位数，较大四分位数对75%分位数。

• 分位数往往取决于数据本身。例如在只有15个数据的样本中，我们可以将数据平均分为15份，不同等分位点值表示不同的分位数值(如下)。

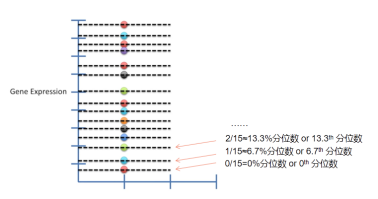
基于分位数的性质，我们可以利用QQ-plot(分位数-分位数图)探究一组数据的分布类型，也可以探究两组数据的分布类型是否一致。

探究数据属于何种分布

• 探究数据属于哪种分布，可以使用QQplot进行探究。例如我们测量15个基因的表达水平，想要探究它属于哪一种分布。首先探究15个基因的表达水平是否属于正态分布：

  • 第一步：绘制数据中每一个基因表达水平的分位数(十五分位数)。

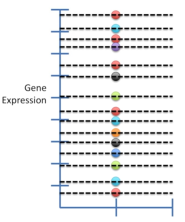
  • 第二步：任意绘制一个标准正态分布曲线。

  • 第三步：在标准正态分布曲线上绘制与已知数据数量相同的分位数(十五分位数)。对于正态分布曲线，将其等分为15份，表示每一区间内发生的概率相等。因为中间数据发生的可能性更大，故中间数据对应的区间较窄，两边数据对应的区间较宽。

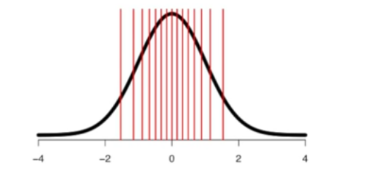
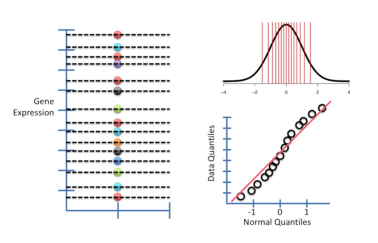
  • 第四步：绘制QQ-plot。QQ-plot为二维图，其中正态分布分位数(Normal Quantiles)来自正态分布(x轴)；数据分位数(Data quantiles)来自真实数据(y轴)。正态分布与未知分布数据分位数值一一对应，将对应结果绘制在QQ-plot中。下图展示1/15分位数值绘制的过程(正态分布的1/15分位数值与真实数据的1/15分位数数值组成第一个点)，其他分位数的绘制方式与之相同。

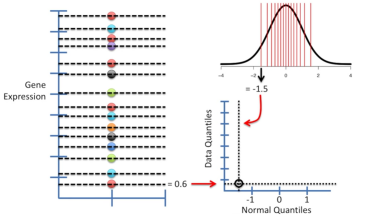
  • 第五步：对新的数据进行直线拟合。如果未知数据为正态分布，那么大多数的点应该位于直线上。在此案例中，直线对该新数据的拟合效果并不是很好(如下图，右下位置)，故这15个基因表达水平量的分布不太可能是正态分布。

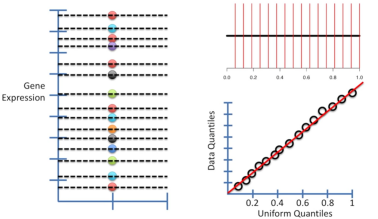
因为这15个基因的表达水平不太可能是正态分布，故接着探究15个基因的表达水平是否属于均匀分布。将假设中的正态分布换成均匀分布，余探究的方法同前，最后得到均匀分布与位置分布数据的QQ-plot(如下图，右下位置)。对新数据进行直线拟合，发现大多数数据位于拟合直线上，故我们可以认为这15个基因表达水平的数据属于均匀分布。

最后，得出结论：与正态分布的QQ-plot相比，我们也更有理由认为这15个基因表达水平的数据属于均匀分布。

探究两组数据的分布是否一致

探索两组数据的分布是否一致，也可以采用QQ图。例如我们一组数据仍然为15个基因的表达水平，另有一组数据仅含4个基因表达水平，我们想要探究这两组数据的分布是否一致。

• 将假设的某种分布类型换成新数据的分位数值，其余步骤同前，对QQ-plot中的结果进行直线拟合。如果大部分数据位于拟合直线上，说明二者的分布类型一致，相反则分布类型不一样。

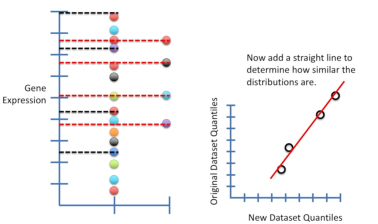
以上展示的是在2组具有少量数据时，探究二者分布类型是否一致。当2组数据更多时，探究二者分布类型是否一致的原理与之相同，我们将会在更多数据中得到更多的分位数和更多的结论。

4.小结

今天和大家一起学习了分位数，及分位数的重要应用——QQ图。相信大家会对熟悉而陌生的QQ图有了更加深刻的印象，在自己的研究数据中能够更加有主见地判断数据分布类型。

参考视频：

1.https://www.youtube.com/watch?v=IFKQLDmRK0Y&list=PLblh5JKOoLUK0FLuzwntyYI10UQFUhsY9&index=32

2.https://www.youtube.com/watch?v=okjYjClSjOg&list=PLblh5JKOoLUK0FLuzwntyYI10UQFUhsY9&index=33

编辑：吕琼

校审：罗鹏